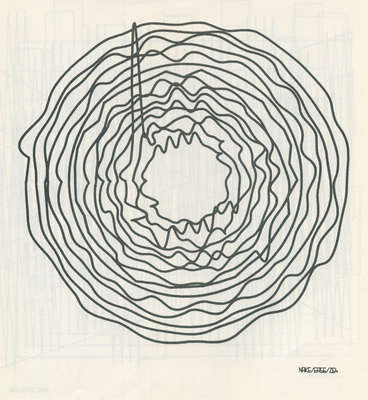
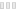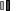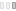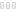This algorithmic drawing is proof of the fact that early “computer art” was in no way restricted to straight lines only. Generated in May of 1965, the drawing owes its existence and, perhaps, its particular character to a simple schema of interpolating randomly chosen points by polynoms (cf. the description of the algorithm).
The drawing consists of 15 individual closed curves. Counting from the outermost inwards, the 6th curve is an undisturbed circle. Outside of it, there are five, inside of it there are nine curves. One of them is a polygon (detect it!).
The method of interpolation, in this case, forced the upwards oriented needle to appear. To be quite clear about this effect: it was not planned in any way. It is a purely algorithmically generated effect. If you like, you could claim this to be a creative decision on behalf of the running algorithm. Nothing would be more stupid than this. Algorithms are neither creative, nor are they not-creative. They are what they are: formal descriptions of computable functions.