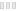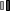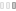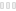Peterson, H. Philip 1965. The Digital Mona Lisa. In: Computers and Automation. Newtonville, Mass. (USA):Berkley Enterprise, Inc.

In this Letter to the Editor, Peterson reacts to – in his view – a certain lack of genuinely digital works in the pages of Computers and Automation when they write about Digital Art.

In the article Peterson describes his technical approach when creating the then very popular image Digital Mona Lisa:

“a – It is composed of square cells, 0.115” on a side. It is 256 cells wide and 390 cells high. (The top and bottom rows contain identification information). Cells are marked off by ticks in the horizontal lines between rows.

b – Each cell contains two decimal digits. The magnitude of these numbers is proportional to the density at points on a color projection slide (.9” by 1.35”) as measured by a CDC 160 computer driving a special high-resolution “jumping spot” scanner. (Actually, 9 bits of density are measured at each point). There are about 100,000 cells in this picture. My research scanner, however, is capable of examining 64 × 10’ points inside a 2” x 2” target area, extracting 9 bits from each, but this much detail would require 12,000 hours to plot using this technique.

c – The number in each cell is the result of scanning 8 points in each tiny area and averaging their densities. About 10’ points were examined which took the CDC 160 about four minutes.

d – The digits are plotted by an incremental plotter driven on-line by a CDC 3200 computer. I designed the font in such a way that the larger the pair of digits are, the darker they appear to the human eye at that cell. Up close to the picture, you see what the computer “sees” – namely a number field; at about 30 feet away, you see the picture shaded as well as a newspaper photograph. (Perhaps a little better, since there are 100 gray levels).

e – It takes about 64 plotter steps to make each digit. The whole picture took about 16 hours to plot and consists of about 16,000,000 plotter steps (300 per second). It was done on a weekend in one continuous computer run."

(This extract of the article is available at [digitalmonalisa.com, n. d.])