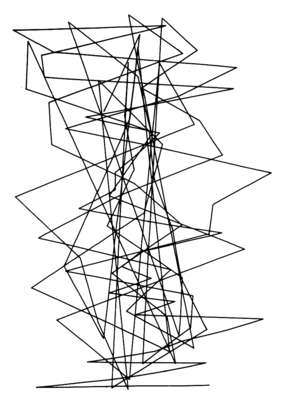
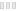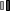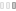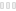" In general, completely random two-dimensional pictures are not very interesting. However the computer is also able to mix together randomness and order in mathematically specified proportions to achieve a desired effect. The intial attempts at such mixing used Gaussian randomness for the X-axis co-ordinates but introduced a specified and non-rendom mathematical function for genrating the Y-axis co-ordinates. Gaussian Quadratic is a particularly good example of this mixing approach. Ninety lines join together 100 points whose horizontal positions are Gaussian. The vertical positions increase quadratically, i.e. the first position has a vertical position from the bottom of the picture given by 1^2 +5 * 1, the second point 2^2 + 5 * 2 , the third point 3^2 + 5 * 3, etc. The maximum picture size is limited to 1024 units wide by 1024 units high, and thus the 30th point would be off the top of the picture (30^2 + 5 * 30 = 1050 ) . To prevent this from happening, the vertical positions at the top are reflected to the bottom of the picture and then continue to rise. the result is a line that starts at the bottom of the picture and randomly zigzags to the top in continually increasing steps; at the top the line is ’ translated’ to the bottomto continue it’s rise. The standard derivation of the Gaussian density is 150. "
Michael A. Noll
Referred from Page 153 Cybernetics, Arts and Ideas